ヤマノケン
ヤマノケンバスタビット等のカジノ系ブロックチェーンゲームを攻略する上で、確率論についてまとめてあるページがあると便利だと思い作成しました。
丁半博打やルーレット、バカラetc…様々な分野にも役立てる事が出来ます。 どんどんこのページを更新していく予定です。
確率論とは
googleで改めて検索した所、
確率論とは、偶然現象に対して数学的な模型を与え、解析する数学の一分野である。 もともとサイコロ賭博といった賭博の研究として始まった。 Wikipedia「確率論」
とあり、確率論自体がもともと賭博(ギャンブル)の研究(攻略)の為に始まったとされています。
確率論そのものの基本的な知識よりも、実戦で疑問に思う事・知っておくべき確率論をまとめたいと思います。
連続で負ける確率

ルーレットにおける赤と黒、バスタビットでの2倍止め狙い、丁半博打等、1/2で勝つ(負ける)ゲームで、連続で負ける確率をまず表にしました。
連続で勝つ確率に置き換える事も出来ます。
| 連続 | 確率 |
|---|---|
| 1 | 50% |
| 2 | 25% |
| 3 | 12.5% |
| 4 | 6.25% |
| 5 | 3.125% |
| 6 | 1.5625% |
| 7 | 0.78125% |
| 8 | 0.390625% |
| 9 | 0.19531% |
| 10 | 0.0976% |
計算式は、1/2のn乗(n連続)で求められます。3回連続なら1/2×1/2×1/2です。
最初は1/2の確率ですから勝つか負けるか分からない勝負も、7回連続で負ける確率は0.78%・・逆に言えば98%の確率で7回連続で負ける事は無いとも言えます。
この事を念頭において次の確率論を学びましょう。
連続の確率論。 連続で丁が出た次に、また丁が出る確率は1/2
では、本題です。

例えば2連続で丁が出た場合、次にまた丁が出る確率は何パーセントでしょうか?
 初心者君
初心者君これは間違いです。正解は50%です。
冷静にイメージしてみましょう。 今からサイコロを1個振ります。

偶数が出る確率は50%です。これは間違いありません。
では、その前に2回連続で偶数が出ていたと聞かされたとします。 そうすると偶数は出にくくなるのでしょうか?
これから振るサイコロの1.2.3.4.5.6のうち、2.4.6.だけが出にくくなるのはイメージしづらいのではないでしょうか。
これから振るサイコロは過去の結果には左右されないのです。 これを確率論の独立性といいます。
つまり、例えばルーレットで赤が連続で10回も続いたとして、これからの勝負で黒の方が当たる確率が高まるというのは間違いです。
例えば、商店街のガラガラくじのように、大きな箱に赤と黒の球が限られた数入っていて、1個ずつ取り出していく場合は、赤の方が沢山出ていれば黒の方が出る確率は上がります。
大数の法則とは
ここで出てくるのが大数の法則というものです。
大数の法則とは、例えばサイコロを振って1が出る確率が1/6だとして、数をこなせばこなすほど結果は1/6に近づいていくという法則です。
先ほどのルーレットに例えると、何度も何度も繰り返せば赤と黒が出る確率は1/2になるという法則です。
 初心者君
初心者君これも間違いです。 黒が出る確率は常に1/2で変わりません。
 初心者君
初心者君残念ながら、これも間違いです。 黒が出る確率は常に1/2で変わりません。
大数の法則で勘違いしやすいのは、「数を重ねれば、赤と黒が同じ数字になるように近づいていく」という解釈です。 これは間違いです。
最初のうちは赤3:黒5というような結果から、数をこなす事で、赤38420:黒37680というような結果になっていくので、どんどん1:1の比率(=1/2の確率)に近づいていくという意味なのです。
【独立性の応用】連続で負けた後に、連続で負ける確率
では、独立性の応用です。
例えば1/2の確率で偶数か奇数かを当てる丁半博打で、5回連続で丁が出る確率は3.12%です。
確率は少ないですが、実際に5回連続くらいなら起こりそうだなというのはイメージ出来ると思います。
これが、10回連続で丁が出る確率となるとその確率は、0.09765625%です。 これはなかなか起こり得ない気がします。
ここで問題です。

既に5回連続で「丁」が出てから、さらに5連続で「丁」が続く確率は何パーセントでしょうか?
こうして実際にイメージしてみると「流石に無い。確率は0.097%だ」と思ってしまいます。
しかし、やはり過去の結果にはとらわれないので、これから5回連続で「丁」が出る確率は3.12%です。0.097%ではありません。
この連続で負ける確率の話はマーチンゲール法等の攻略法においてとても重要です。
マーチンゲール法は、確率1/2のギャンブルで、例えば10万2300円の資金を用意して100円ずつベットすれば、10連敗さえしなければ必ず勝てるという攻略法です。
すると、確率を上げるために「毎回、3回連続で丁が出た後に半を賭け続ける事」等というルールが生まれがちですが、これには全く意味が無いという事になります。
バスタビットでも、「●倍以下が連続で続いてからベットをする」というような事が書かれてある攻略法があったとしたら、それは確率論的には間違っています。
ただしバスタビットはゲームですから必ずしもその攻略法が間違っているとは限りません。
勝率1/3のギャンブルで連続で負ける確率
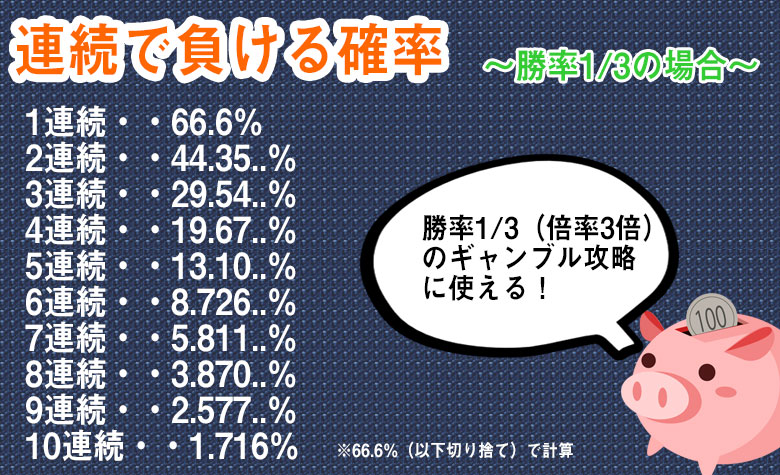
モンテカルロ法やココモ法を使う時に必要な、倍率3倍(負ける確率2/3)の時に連続で負ける確率表です。
1/3の確率で勝つ(2/3で負ける)という場合は、連続で負ける確率2/3×2/3×2/3・・という計算方法になります。
連続で勝つ確率よりも、連続で負ける確率の方を使う事が多いので「負ける」確率を表しました。
1/100の確率で当たりの時、100回繰り返して当たる確率
例えば、1/100の確率で当たりのキャラクターが出るソーシャルゲームのガチャがあったとします。
店舗に置いてあるようなガチャガチャの時は1回ごとに1個減っていくので100回回せば必ず1回は当たりが出ますが、独立性の話があったように、毎回1/100の確率でガチャをする場合、100回で当たる確率は何パーセントになるのか考えてみましょう。
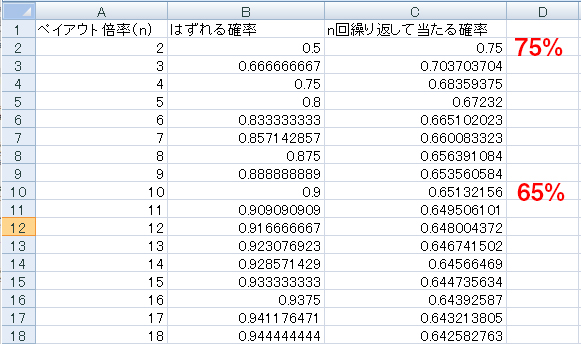
結論から先に行ってしまうと、100回だと63.39%くらいです。Excelで計算してみました。
計算方法は、
- ペイアウト倍率=n倍の時、外れる確率は1/nです。
- n回繰り返すので1/nのn乗が、全て外れる確率です。
- ここでは全体の数字を1(例:1/2)としているので、1から全て外れる確率を引くと、当たる確率になります。
確認やイメージを深める為に例えば、倍率2倍・確率1/2のギャンブルで当たる確率で答え合わせをしてみましょう。
1回目と2回目のパターンは4パターンです。 このうち、偶数を当たりとした場合
| パターン1 | 偶数・奇数 |
|---|---|
| パターン2 | 偶数・偶数 |
| パターン3 | 奇数・奇数 |
| パターン4 | 奇数・偶数 |
奇数・奇数のパターン以外は偶数が1回は出ていますので、外れる確率は1/4(25%)です。
つまり、当たる確率は、100-25=75%となり、表の数字と合致。 3倍でも4倍でも同じです。
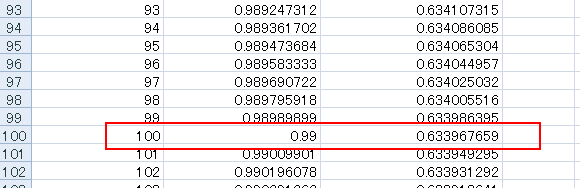
では、100回の場合はどうなるでしょうか? 数字が上からどんどん下がってきているのでかなり低い数字になるのかというと、そうでもなく0.633967659という数字になっており、1を全体の数字としているので、100倍すると63.339%となります。
先入観だと、1/100は100%とか、出るか出ないかの50%等と思ってしまいがちですが、意外と中途半端な数字になる所が面白いです。